Alexandrian Patterns

Alexandrian Patterns

In the context of TameFlow, the word “pattern” is used and intended in a very technical way, as an Alexandrian Pattern (a.k.a. “Alexandrine Pattern”). The canonical and most widely accepted definition of an Alexandrian Pattern is [ALEXANDER-1979]:

[A] pattern is a three-part rule, which express a relation between a certain context, a problem, and a solution.

Introduction to Alexandrian Patterns

To understand what it means that a pattern is a “solution to a problem in a context” let us consider some simple examples which are tangible and easy to relate to. Suppose you are constructing a building and have identified a problem, like: “Allow natural light into a building.” And you notice a recurring solution, like “make an opening in a wall.”

However, the context where you apply the solution to the problem is important. For instance, if you are considering a primitive mud hut or a modern skyscraper, the pattern might have different significances and implications. The context is an integral component of a pattern. The two cases effectively determine two different patterns:

Pattern 1:
    Context: Mud Hut
    Problem: Allow natural light into the building
    Solution: Make an opening in the wall

Pattern 2:
    Context: Skyscraper
    Problem: Allow natural light into the building
    Solution: Make an opening in the wall

While the two patterns share the same problem and even the same solution, the fact that they have a different context is significant enough to make them distinct. This becomes evident considering that the application of one pattern may become the context of another pattern.

Suppose you now notice a new problem. You need to “prevent wind from entering” the building. This problem is a consequence of the application of the earlier pattern, where you created an opening in the wall. The solution could be very different, though, depending on the original context. For instance it could be: “put palm leaves in front of the opening” for the mud hut, or “add glass windows to the opening” for the skyscraper.

Two distinct contexts (mud hut or skyscraper) had a common problem (need for natural light) and a common solution (opening in wall). The application of the solution to the problem — creating an opening in the wall to allow natural light into the building — became the context where a further problem (prevent wind from entering) had two distinct solutions (palm leaves or window). We have thus further identified the following patterns:

Pattern 3:
    Context: Pattern 1
    Problem: Prevent wind from entering
    Solution: Put palm leaves in front of the opening

Pattern 4:
    Context: Pattern 2
    Problem: Prevent wind from entering
    Solution: Add glass windows to the opening

Because the application of one pattern becomes the context for the application of further patterns, and so on, it becomes possible to express solutions through a sequence of patterns, like:

    [Pattern 1] -> [Pattern 3]

Or:

    [Pattern 2 ] -> [Pattern 4]

In this way, patterns are like words in a language that can be used to describe a general solution. The sequence of valid pattern applications become like sentences that describe the solution in more detail. So, the “sentence” [Pattern 1] -> [Pattern 3] becomes a shorthand meaning: “You have a mud hut, you need to get natural light inside. You create an opening to let the light in, but then you need to prevent wind from blowing inside, so you put palm leaves in front of the opening!” Likewise, the “sentence” [Pattern 2] -> [Pattern 4] means… exactly what you can infer!

The true power of Alexandrian Patterns is not in the patterns in isolation, by themselves; but in their combination through this sort of language — a Pattern Language. Pattern language construction is very much based on observations of reality. You start by noting if there are any “normal” patterns, and recognize recurrences of configurations, structures, behaviors or other elements that are relevant to your domain. You need to be particularly attentive to find those repeating elements that are recurring problems and/or recurring solutions. You will have a list of candidate “Alexandrian” patterns; at which point you can examine the “normal” patterns in order to determine if they can be associated with all the features that characterize “Alexandrian” patterns. (We will see this process in more detail later.)

The pattern language is constructed by defining the “resulting context” of a pattern, and listing any related patterns. For instance, in the above example, [Pattern 3] would be listed as a related pattern within the description on [Pattern 1]. (A pattern can have any number of related patterns, and not only one as in this introductory example.)

Related patterns are those that become relevant after the “application” of any given pattern. It is the linkage between one pattern and its related patterns that define the rules (like a grammar) of the pattern language. So the definition of the first two patterns might be extended as follows:

Pattern 1:
    Context: Mud Hut
    Problem: Allow natural light into the building
    Solution: Make an opening in the wall
    Related: Pattern 3

Pattern 2:
    Context: Skyscraper
    Problem: Allow natural light into the building
    Solution: Make an opening in the wall
    Related: Pattern 4

The network of patterns constructed this way represents the pattern language. You may express an overall solution in such a pattern language by stating (like sentences in ordinary language) a sequence of application of patterns. In the redefined example, we see that [Pattern 1] can be combined with [Pattern 3]; and [Pattern 2] can be combined with [Pattern 4]. So according to the grammar rules of this simple language, the sentence [Pattern 2] -> [Pattern 3] would be invalid. In fact, putting palm leaves on the openings of a skyscraper does not make much sense, does it?

The situation described can be illustrated schematically as follows:

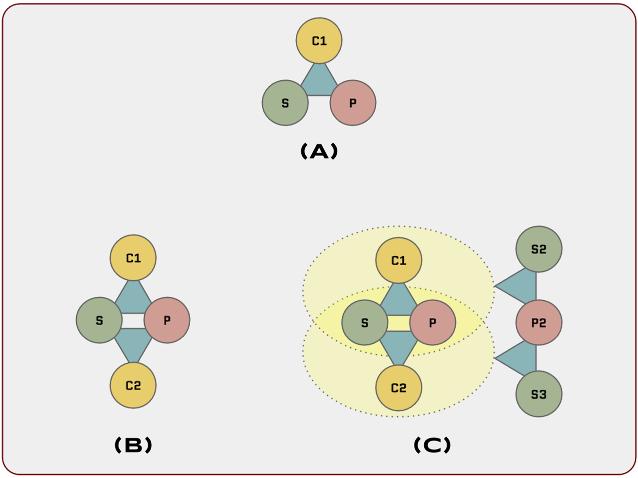
In the figure, we can see the following:

• Diagram A illustrates one pattern, where C1 is the context, P is the problem and S is the solution. The pattern can also be written as {C1, P, S}.

• Diagram B shows that the same problem P and solution S can refer to a different context C2. This defines a second pattern, {C2, P, S}.

• Diagram C shows how the two previous patterns become the context of two other patterns, which share a problem P2 but have different solutions S2 and S3. The two new patterns can be denoted, respectively, as: {{C1, P, S}, P2, S2} and {{C2, P, S}, P2, S3}.

In the remainder of this Chapter we will get further acquainted with patterns, pattern languages and pattern theory.

More about Alexandrian Patterns

Patterns are abstract solutions to a problem in a context. Patterns provide a formal method for documenting and capturing tacit knowledge [CLOUTIER-2006]. They allow to capture the implicit knowledge of experts about their practices, and document them in systematic way, typically with a Pattern Catalog. Patterns illustrate the reasons that support specific design decisions. Patterns allow to describe and communicate about good designs, so that others can reuse them. Patterns enable communication about complex systems.

Patterns are concepts [ALEXANDER-1964]. Patterns represent a single idea. Good patterns solve specific problems. They are not neutral observations. Patterns expose the unbalanced forces that create problems. Patterns present diagnoses of genuine problems and plausible prescriptions and actions to correct them [SCHULER-2008].

Patterns are based on proven ideas; though the solution is not immediately obvious. Often the solution is derived and generated indirectly through the application of a sequence of patterns in a specific order. Patterns are like heuristics, and they provide guidance for dealing with complex system. They represent relationships between deeper structures of a complex system; thus patterns are interrelated among themselves. In Alexander’s view patterns are similar to genetic code, and just like genetic code can generate complex organisms, patterns can generate complex, higher order structures [ALEXANDER-1999].

Patterns address complex issues. They are not templates that can just be mindlessly copied [SALINGAROS-2000]. They need application and combination to arrive at solutions. Copying templates require no intellectual effort beyond intuitive matching. Using patterns implies making difficult decisions about complex interactions between the designed artifacts and humans [SALINGAROS-2000].

Patterns are the building blocks of a true language. This kind of language is called a Pattern Language: a complete language with its own vocabulary, syntax, grammar, ontology and taxonomy. A pattern language is a network of interconnected patterns, which can be used to describe a comprehensive design at different scales, and from different viewpoints. Pattern languages allow to arrange complex and interrelated abstract ideas in a logical, tractable and reasonable way [SCHULER-2008]. Patterns can be combined in infinite ways, just like the words of our languages are combined to form sentences, convey broader meaning and allow representing major thoughts as we do with all our forms of writing (from poetry to scientific treatises).

Patterns have a context. They do not exist in a vacuum (like ordinary patterns). They are inevitably connected to other patterns: larger ones above, and smaller below; or containers and encapsulated ones. Patterns can be composed. Patterns can decorate or embellish one another. Patterns are not confining or delimiting (as ordinary, “cookie-cutter” patterns).

Patterns are reusable. Pattern , being an abstract solution to a problem, can be adapted and reused in practice in infinite ways, through one’s own instance of the abstract pattern, adapted to one’s own special situation and context, specifically through the combination with other patterns. When patterns are applied, due to their generative nature, results are never the same. [ALEXANDER-1999] explains that a few patterns can generate an organic variety and a multitude of complex structures:

[This is] because the generative scheme always generates structure that starts with the existing context, and creates things which relate directly and specifically to that context.